MBCF & SVD
Model based Collaborative Filtering(MBCF)
MBCF의 정의와 원리, SVD원리에 대해 배우자.
NBCF의 한계
- Sparsity(희소성) 문제
- 데이터가 충분하지 않다면 추천 성능이 떨어짐.
- 데이터가 부족하거나 혹은 아예 없는 유저, 아이템의 경우 추천이 불가능하다.
- Saclability(확장성) 문제
- 유저와 아이템이 늘어날수록 유사도 계산이 늘어난다.
- 유저, 아이템이 많아야 정확한 예측을 하지만 반대로 시간이 오래 걸린다.
모델 기반 협업 필터링(MBCF)
항목 간 유사성을 단순 비교하는 것이 아니라 데이터에 내재한 패턴을 이용해 추천하는 CF 기법
- Parametric Machine Learning을 사용
- 주어진 데이터를 사용해 모델 학습
- 데이터 정보가 파라미터의 형태로 모델에 압축
- 모델의 파라미터는 데이터의 패턴을 나타내고, 최적화를 통해 업데이트
특징
- 데이터에 숨겨진 유저-아이템 관계의 잠재적 특성/패턴을 찾음
- 현업에서는 Matrix Factorization 기법이 많이 사용됨
- 특히 최근에는 MF원리를 Deep Learning 모델에 응용해 성능을 냄.
장점
- 모델 학습/서빙
- 이미 학습된 모델을 가지고 서빙하기 때문에 속도가 빠르다.
- Sparsity / Scalability 문제 개선
- sparse 한 데이터에서도 좋은 성능을 보임
- 사용자, 아이템 수가 늘어나도 좋은 추천 성능을 보임.
- Overfitting 방지
- 전체 데이터의 패턴을 학습하기 때문 이웃 기반 CF와 비교시 오버피팅 덜된다.
- Limited Coverage 극복
- 이웃 기반 CF의 경우 공통의 유저 / 아이템을 많이 공유해야만 유사도 값이 정확해짐
- NBCF의 유사도 값이 정확하지 않은 경우 이웃의 효과를 보기 어려움.
Latent Factor Model
- 유저와 아이템의 관계를 잠재적 요인으로 표현 할 수 있다고 보는 모델
- 다양하고 복잡한 유저와 아이템의 특성을 몇 개의 벡터로 compact하게 표현
- 유저-아이템 행렬을 저차원의 행렬로 분해하는 방식으로 작동
- 각 차원의 의미는 모델 학습을 통해 생성되며 표면적으로는 알 수 없음.
- 같은 벡터 공간에서 유저와 아이템 벡터가 놓일 경우 유저와 아이템의 유사한 정도를 확인할 수 있음.
- 유저 벡터와 아이템 벡터가 유사하게 놓인다면 해당 유저에게 해당 아이템이 추천될 확률이 높음.
예시
SVD
- Singular Vector Decomposition(SVD)
- 선형 대수학에서 차원 축소 기법 중 하나로 분류됨
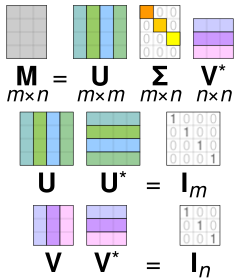wikipedia
SVD 개념
Rating Matrix R 에 대해 유저와 아이템의 잠재 요인을 포함할 수 있는 행렬로 분해
- 유저 잠재 요인 행렬
- 잠재 요인 대각행렬
- 아이템 잠재 요인 행렬
Full SVD: \(R = U\sum V^T\)
- U : 유저와 Latent Factor의 관계
- V : 아이템과 Latent Factor의 관계
- \(\sum\) : Latent Factor의 중요도를 나타냄
- 아래 그림은 Truncated SVD, Full SVD를 축소한 느낌.
- 대표값으로 사용될 k개의 특이치만 사용함.
- \(R \approx \hat{R}\) 최대한 유사한 Full SVD
- 유추는 가능하지만 정확히 무엇을 의미하는지는 알 수 없음.
한계점
- 분해하려는 행렬의 knowledge가 불완전할 때 정의되지 않음.
- 따라서 결측된 entry를 모두 채우는 Imputation을 통해 Dense Matrix를 만들어 SVD를 수행함.
- 0이나 평균 평점으로 채운다.
- 데이터 왜곡시킨다.
- 행렬의 entry가 매우 적을 때 SVD를 적용하면 과적합 되기 쉬움
-> SVD의 원리를 차용하되, 다른 접근법이 필요 -> Matrix Factorization의 등장!
Comments